Bit de paridad
3 de marzo de 2023
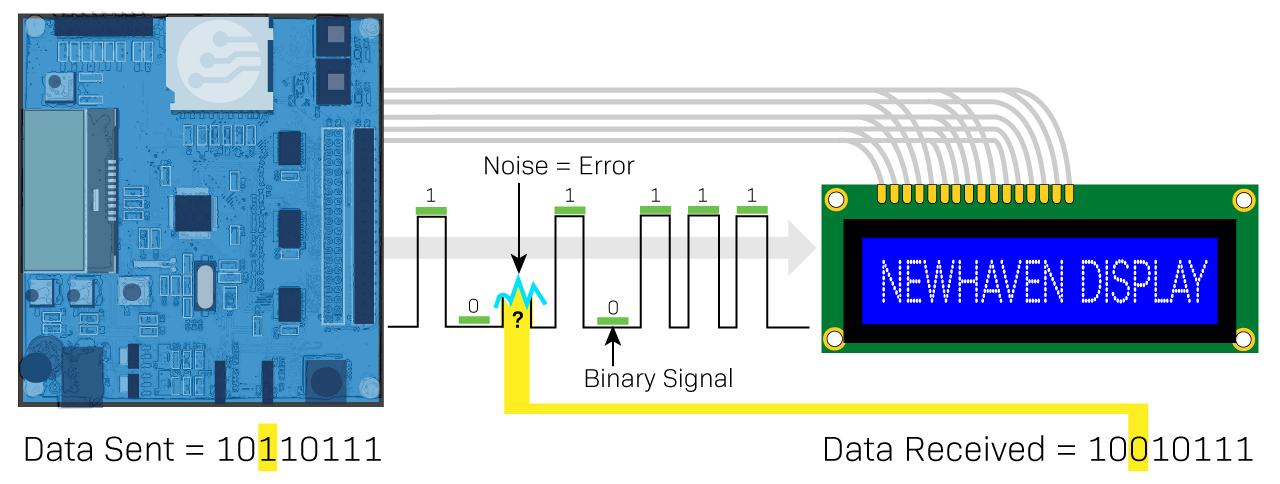
Errors in binary communication refers to situations where the message received differs from the message intended to be transmitted. This can occur for various reasons, such as poor signal integrity, noise, or system failures. The errors can lead to incorrect interpretations of the message and affect the accuracy and reliability of a digital signal communication. One solution to reducing binary communication errors is the use of a parity bit.
En este artículo:
¿Qué es el bit de paridad?
Un bit de paridad, también denominado comprobación de paridad, es un bit adicional que se añade a un conjunto de bits de datos binarios con el fin de detectar errores durante la transmisión de datos. El bit de paridad se utiliza para comprobar si el número de 1s en una cadena de datos es par o impar, dando lugar a dos tipos: bit de paridad par y bit de paridad impar.
Errores binarios
Un error en la comunicación binaria se produce cuando un 1 se convierte inesperadamente en un 0 o viceversa.
Learn more: Serial data communication standard RS232
Paridad par
En un sistema de paridad par, el bit de paridad se establece en 1 o 0, de modo que el número total de bits de 1, incluido el bit de paridad, sea un número par.
Cómo calcular la paridad par
Si el número de 1s en la cadena de datos es impar, el bit de paridad se pone a 1 para garantizar que el número total de 1s, incluido el bit de paridad, sea par. Si el número de 1s en la cadena de datos ya es par, el bit de paridad se pone a 0.
Paridad impar
En un sistema de paridad impar, el bit de paridad se establece en 1 o 0, de modo que el número total de bits de 1, incluido el bit de paridad, se convierte en un número impar.
Cómo calcular la paridad impar
Si el número de 1s en la cadena de datos es par, el bit de paridad se pone a 1 para asegurar que el número total de 1s, incluyendo el bit de paridad, es impar. Si el número de 1s en la cadena de datos ya es impar, el bit de paridad se pone a 0.
Ejemplos de bits de paridad
| Cadena de datos de 7 bits | Número de bits 1 | 8 bits, incluido el bit de paridad | |
|---|---|---|---|
| paridad par | paridad impar | ||
| 0000000 | 0 | 00000000 | 00000001 |
| 1100001 | 3 | 11000011 | 11000010 |
| 1100101 | 4 | 11001010 | 11001011 |
| 1111111 | 7 | 11111111 | 11111110 |
La comprobación del bit de paridad se utiliza habitualmente en la transmisión de caracteres ASCII, donde el 8º bit se reserva como bit de paridad mientras que los 7 bits restantes se utilizan para codificar el carácter.
Cómo funciona el bit de paridad
Antes de transmitir datos, tanto el emisor como el receptor deben ponerse de acuerdo sobre la paridad par o impar. Antes de enviar cada paquete de datos (cadena de bits), el emisor calcula su bit de paridad (0 ó 1) para asegurarse de que coincide con la paridad acordada (par o impar). Al recibirlo, el receptor comprueba la paridad de los datos recibidos con la paridad esperada. Si no coinciden, indica un error, y los datos pueden descartarse o corregirse solicitando una retransmisión.
El bit de paridad sólo se utiliza para ayudar a detectar errores, pero carece de la capacidad de rectificar cualquier error porque no puede identificar el bit corrupto específico. Por lo tanto, la única opción para corregir errores es descartar toda la cadena de datos y solicitar una nueva transmisión al remitente.
Posición del bit de paridad
Aunque no hay una regla establecida para la posición del bit de paridad, por convención se suele añadir al final del mensaje de cadena binaria.
Detección de errores
La comprobación de paridad en el receptor puede detectar errores comparando la paridad de la señal recibida con la paridad esperada. Si no coincide, el receptor puede solicitar una retransmisión al transmisor.
Detectar si el número de 1s en una cadena de datos binarios es par o impar puede calcularse mediante el operador Módulo. Modulo, o "mod", es una operación matemática que halla el resto cuando un número entero se divide por otro. La operación Modulo se representa mediante el símbolo %.
Utilizando Modulo, podemos determinar si un número es par si se puede dividir por 2 sin que quede resto. En cambio, si un número deja un resto al dividirlo por 2, se considera impar.
El siguiente ejemplo de programa en C ilustra el proceso de comprobación de la paridad utilizando el módulo:
#includeint main() { unsigned char byte; int num_ones = 0; printf("Enter a byte (in decimal): "); scanf("%hhu", &byte); // Count the number of 1s in the byte for (int i = 0; i < 8; i++) { if ((byte >> i) & 1) { num_ones++; } } // Detect parity with mod 2 and print the parity type. if (num_ones % 2 == 0) { // printf("Even parity\n"); } else { printf("Odd parity\n"); } return 0; }
El programa comienza leyendo un byte del usuario. A continuación, utiliza un bucle para contar el número de bits 1 en el byte. Esto se hace desplazando el byte a la derecha en cada posición de bit (de 0 a 7) y comprobando si el bit resultante es 1. Si lo es, se incrementa la cuenta de 1 bits. Finalmente, el programa comprueba si el número de 1 bits es par o impar, e imprime el mensaje apropiado.
Observe que el programa utiliza un unsigned char para almacenar el byte, que es un entero de 8 bits que puede contener valores entre 0 y 255. El especificador de formato %hhu se utiliza con scanf() para leer un valor de byte del usuario.
Cómo añadir un bit de paridad
Examinemos un ejemplo en el que necesitamos transmitir la cadena de datos 1100101. En primer lugar, contamos el número de 1s en la cadena de datos y determinamos si el recuento es par o impar utilizando el operador mod con 2 como divisor:
(1+1+0+0+1+0+1) mod 2
4 mod 2 = 0
Como 4 dividido por 2 no tiene resto, el resultado es 0, lo que indica que tenemos un número par de 1. Si hemos acordado una paridad par, añadimos un "0" como bit de paridad al final del mensaje, lo que da como resultado 11001010, que ya puede enviarse. Alternativamente, si hemos acordado paridad impar, invertimos el bit de paridad y añadimos un "1" en su lugar, resultando 11001011 como mensaje final que puede ser transmitido.
Usos del bit de paridad
- Detección de errores: Uno de los principales usos de los bits de paridad es detectar errores durante la transmisión de datos.
- Almacenamiento en memoria: Los bits de paridad también se utilizan en los sistemas de memoria de los ordenadores para detectar errores cuando los datos se almacenan en la memoria. Cuando los datos se almacenan en memoria, siempre existe el riesgo de que se produzcan errores debido a diversos factores, como interferencias electromagnéticas, fallos de hardware, etc.
- Sistemas RAID: El bit de paridad también se utiliza en los sistemas RAID (Redundant Array of Inexpensive Disks). RAID también puede denominarse "Redundant Array of Independent Drives". Los sistemas RAID utilizan varios discos para almacenar datos de forma redundante y proteger contra fallos de disco. Utilizan paridad para la tolerancia a fallos.
Más información: EMI (interferencias electromagnéticas)
Conclusión
En conclusión, el bit de paridad es un mecanismo de detección de errores sencillo pero eficaz que puede ayudar a garantizar la precisión del almacenamiento y la transmisión de datos. Aunque los bits de paridad no son infalibles y sólo pueden detectar algunos errores, siguen siendo útiles para muchas aplicaciones en las comunicaciones binarias de datos.


