Paritätsbit
3. März 2023
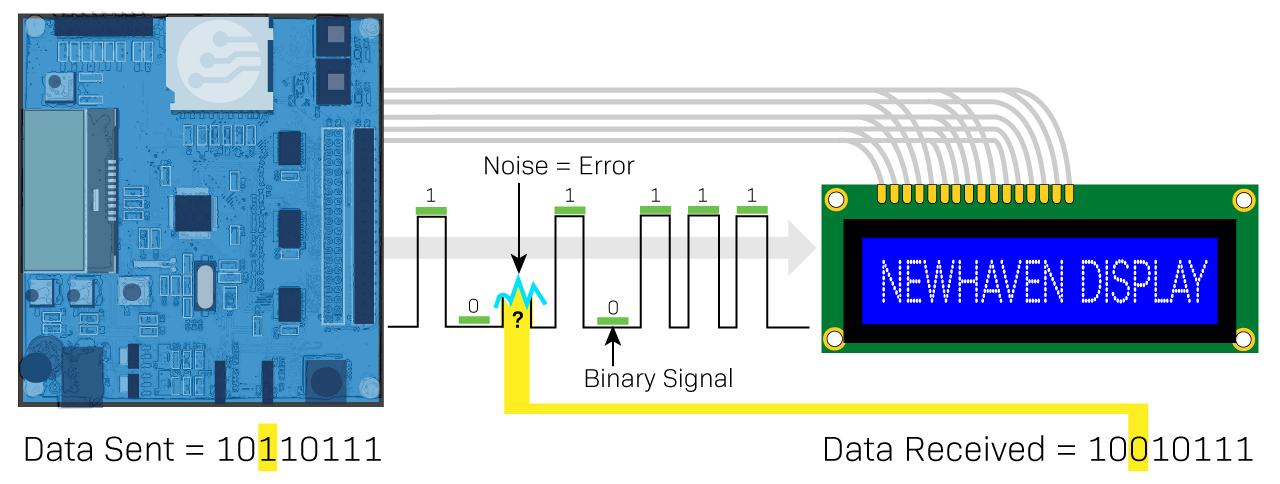
Errors in binary communication refers to situations where the message received differs from the message intended to be transmitted. This can occur for various reasons, such as poor signal integrity, noise, or system failures. The errors can lead to incorrect interpretations of the message and affect the accuracy and reliability of a digital signal communication. One solution to reducing binary communication errors is the use of a parity bit.
In diesem Artikel:
Was ist ein Paritätsbit?
Ein Paritätsbit, auch Paritätsprüfung genannt, ist ein zusätzliches Bit, das zu einer Reihe von binären Datenbits hinzugefügt wird, um Fehler bei der Datenübertragung zu erkennen. Das Paritätsbit wird verwendet, um zu prüfen, ob die Anzahl der 1en in einer Datenkette gerade oder ungerade ist, was zu zwei Arten führt: gerades Paritätsbit und ungerades Paritätsbit.
Binäre Fehler
Ein Fehler in der binären Kommunikation tritt auf, wenn sich eine 1 unerwartet in eine 0 verwandelt oder andersherum.
Learn more: Serial data communication standard RS232
Gerade Parität
In einem System mit gerader Parität wird das Paritätsbit entweder auf 1 oder 0 gesetzt, so dass die Gesamtzahl der 1-Bits, einschließlich des Paritätsbits, eine gerade Zahl ergibt.
Wie berechnet man eine gerade Parität?
Wenn die Anzahl der 1en im Datenstring ungerade ist, wird das Paritätsbit auf 1 gesetzt, um sicherzustellen, dass die Gesamtzahl der 1en, einschließlich des Paritätsbits, gerade ist. Wenn die Anzahl der 1en im Datenstring bereits gerade ist, wird das Paritätsbit auf 0 gesetzt.
Ungerade Parität
In einem System mit ungerader Parität wird das Paritätsbit entweder auf 1 oder 0 gesetzt, so dass die Gesamtzahl der 1-Bits, einschließlich des Paritätsbits, eine ungerade Zahl ergibt.
Wie man die ungerade Parität berechnet
Wenn die Anzahl der 1en im Datenstring gerade ist, wird das Paritätsbit auf 1 gesetzt, um sicherzustellen, dass die Gesamtzahl der 1en, einschließlich des Paritätsbits, ungerade ist. Wenn die Anzahl der 1en im Datenstring bereits ungerade ist, wird das Paritätsbit auf 0 gesetzt.
Beispiele für Paritätsbits
| Datenstring mit 7 Bits | Anzahl der 1-Bits | 8 Bits einschließlich des Paritätsbits | |
|---|---|---|---|
| gerade Parität | ungerade Parität | ||
| 0000000 | 0 | 00000000 | 00000001 |
| 1100001 | 3 | 11000011 | 11000010 |
| 1100101 | 4 | 11001010 | 11001011 |
| 1111111 | 7 | 11111111 | 11111110 |
Die Paritätsbitprüfung wird häufig bei der Übertragung von ASCII-Zeichen verwendet, wobei das 8. Bit als Paritätsbit reserviert ist, während die restlichen 7 Bits zur Codierung des Zeichens verwendet werden.
Wie das Paritätsbit funktioniert
Vor der Übertragung von Daten müssen sich Sender und Empfänger auf eine gerade oder ungerade Parität einigen. Vor dem Senden jedes Datenpakets (Bitfolge) berechnet der Sender sein Paritätsbit (0 oder 1), um sicherzustellen, dass es mit der vereinbarten Parität (ungerade oder gerade) übereinstimmt. Beim Empfang prüft der Empfänger die Parität der empfangenen Daten mit der erwarteten Parität. Wenn sie nicht übereinstimmen, liegt ein Fehler vor, und die Daten können verworfen oder durch Anforderung einer erneuten Übertragung korrigiert werden.
Das Paritätsbit wird nur zur Fehlererkennung verwendet, kann aber keine Fehler beheben, da es das beschädigte Bit nicht identifizieren kann. Die einzige Möglichkeit, Fehler zu beheben, besteht also darin, die gesamte Datenfolge zu verwerfen und den Absender um eine erneute Übertragung zu bitten.
Position des Paritätsbits
Obwohl es keine feste Regel für die Position des Paritätsbits gibt, wird es üblicherweise am Ende der binären Zeichenfolge hinzugefügt.
Fehlererkennung
Die Paritätsprüfung am Empfänger kann Fehler erkennen, indem sie die Parität des empfangenen Signals mit der erwarteten Parität vergleicht. Im Falle einer Abweichung kann der Empfänger eine erneute Übertragung vom Sender anfordern.
Ob die Anzahl der 1en in einer binären Datenkette gerade oder ungerade ist, kann mit dem Modulo-Operator berechnet werden. Modulo, oder "mod", ist eine mathematische Operation, die den Rest ermittelt, wenn eine ganze Zahl durch eine andere geteilt wird. Die Modulo-Operation wird durch das Symbol % dargestellt.
Mit Modulo können wir feststellen, ob eine Zahl gerade ist, wenn sie ohne Rest durch 2 geteilt werden kann. Bleibt dagegen bei einer Zahl ein Rest übrig, wenn sie durch 2 geteilt wird, gilt sie als ungerade.
Das folgende C-Programmbeispiel veranschaulicht den Prozess der Paritätsprüfung mit Modulo:
#includeint main() { unsigned char byte; int num_ones = 0; printf("Enter a byte (in decimal): "); scanf("%hhu", &byte); // Count the number of 1s in the byte for (int i = 0; i < 8; i++) { if ((byte >> i) & 1) { num_ones++; } } // Detect parity with mod 2 and print the parity type. if (num_ones % 2 == 0) { // printf("Even parity\n"); } else { printf("Odd parity\n"); } return 0; }
Das Programm beginnt mit dem Einlesen eines Bytes vom Benutzer. Anschließend zählt es in einer Schleife die Anzahl der 1-Bits im Byte. Dazu wird das Byte um jede Bitposition (0 bis 7) nach rechts verschoben und geprüft, ob das resultierende Bit 1 ist. Ist dies der Fall, wird die Anzahl der 1-Bits erhöht. Schließlich prüft das Programm, ob die Anzahl der 1-Bits gerade oder ungerade ist, und gibt die entsprechende Meldung aus.
Beachten Sie, dass das Programm ein vorzeichenloses Zeichen verwendet, um das Byte zu speichern, das eine 8-Bit-Ganzzahl ist, die Werte zwischen 0 und 255 enthalten kann. Der %hhu-Formatbezeichner wird mit scanf() verwendet, um einen Byte-Wert vom Benutzer einzulesen.
Wie man ein Paritätsbit hinzufügt
Betrachten wir ein Beispiel, bei dem wir die Datenfolge 1100101 übertragen müssen. Zunächst zählen wir die Anzahl der 1en im Datenstring und bestimmen, ob die Anzahl gerade oder ungerade ist, indem wir den Mod-Operator mit 2 als Divisor verwenden:
(1+1+0+0+1+0+1) mod 2
4 mod 2 = 0
Da 4 geteilt durch 2 keinen Rest hat, ist das Ergebnis 0, was anzeigt, dass wir eine gerade Anzahl von 1en haben. Wenn wir uns auf eine gerade Parität geeinigt haben, hängen wir eine "0" als Paritätsbit an das Ende der Nachricht an, was 11001010 ergibt, die nun gesendet werden kann. Wenn wir uns auf eine ungerade Parität geeinigt haben, kehren wir das Paritätsbit um und hängen stattdessen eine "1" an, was zu 11001011 als endgültige Nachricht führt, die übertragen werden kann.
Verwendung von Paritätsbits
- Fehlererkennung: Eine der Hauptaufgaben von Paritätsbits ist die Erkennung von Fehlern bei der Datenübertragung.
- Speicherung im Speicher: Paritätsbits werden auch in Computerspeichersystemen verwendet, um Fehler bei der Speicherung von Daten im Speicher zu erkennen. Bei der Speicherung von Daten im Speicher besteht immer die Gefahr von Fehlern, die durch verschiedene Faktoren wie elektromagnetische Störungen, Hardwarefehler usw. verursacht werden.
- RAID-Systeme: Das Paritätsbit wird auch in Redundant Array of Inexpensive Disks (RAID) verwendet. RAID kann auch als "Redundant Array of Independent Drives" bezeichnet werden. RAID-Systeme verwenden mehrere Festplatten, um Daten redundant zu speichern und vor Festplattenfehlern zu schützen. Sie verwenden Parität für Fehlertoleranz.
Erfahren Sie mehr: EMI (Elektromagnetische Interferenz)
Schlussfolgerung
Zusammenfassend lässt sich sagen, dass das Paritätsbit ein einfacher, aber wirksamer Fehlererkennungsmechanismus ist, der die Genauigkeit der Speicherung und Datenübertragung gewährleisten kann. Obwohl Paritätsbits nicht narrensicher sind und nur einige Fehler erkennen können, sind sie für viele Anwendungen in der binären Datenkommunikation nützlich.


