Bit de parité
3 mars 2023
Errors in binary communication refers to situations where the message received differs from the message intended to be transmitted. This can occur for various reasons, such as poor signal integrity, noise, or system failures. The errors can lead to incorrect interpretations of the message and affect the accuracy and reliability of a digital signal communication. One solution to reducing binary communication errors is the use of a parity bit.
Dans cet article :
Qu'est-ce qu'un bit de parité ?
Un bit de parité, également appelé contrôle de parité, est un bit supplémentaire ajouté à un ensemble de bits de données binaires dans le but de détecter les erreurs lors de la transmission de données. Le bit de parité est utilisé pour vérifier si le nombre de 1 dans une chaîne de données est pair ou impair, ce qui donne deux types de bits : le bit de parité pair et le bit de parité impair.
Erreurs binaires
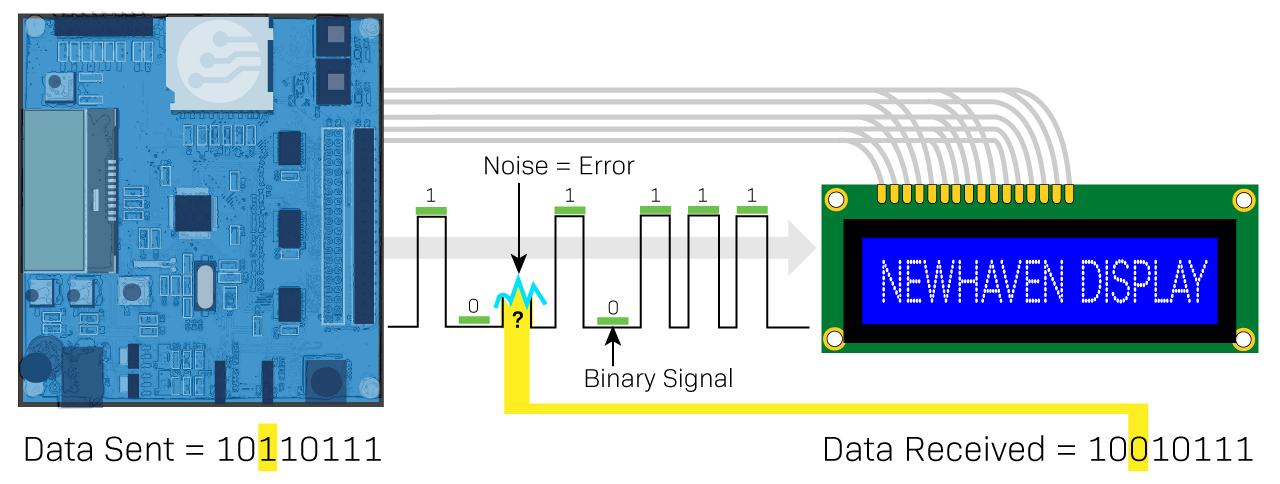
Une erreur dans la communication binaire se produit lorsqu'un 1 se transforme inopinément en 0 ou vice versa.
Learn more: Serial data communication standard RS232
Parité paire
Dans un système de parité paire, le bit de parité est mis à 1 ou à 0 de sorte que le nombre total de bits 1, y compris le bit de parité, devient un nombre pair.
Comment calculer la parité paire
Si le nombre de 1 dans la chaîne de données est impair, le bit de parité est mis à 1 pour garantir que le nombre total de 1, y compris le bit de parité, est pair. Si le nombre de 1 dans la chaîne de données est déjà pair, le bit de parité est mis à 0.
Parité impaire
Dans un système à parité impaire, le bit de parité est mis à 1 ou à 0 de sorte que le nombre total de bits 1, y compris le bit de parité, devient un nombre impair.
Comment calculer la parité impaire
Si le nombre de 1 dans la chaîne de données est pair, le bit de parité est mis à 1 pour garantir que le nombre total de 1, y compris le bit de parité, est impair. Si le nombre de 1 dans la chaîne de données est déjà impair, le bit de parité est mis à 0.
Exemples de bits de parité
| Chaîne de données de 7 bits | Nombre de bits 1 | 8 bits, y compris le bit de parité | |
|---|---|---|---|
| parité paire | parité impaire | ||
| 0000000 | 0 | 00000000 | 00000001 |
| 1100001 | 3 | 11000011 | 11000010 |
| 1100101 | 4 | 11001010 | 11001011 |
| 1111111 | 7 | 11111111 | 11111110 |
Le contrôle du bit de parité est couramment utilisé dans la transmission de caractères ASCII, où le 8e bit est réservé comme bit de parité tandis que les 7 bits restants sont utilisés pour coder le caractère.
Fonctionnement du bit de parité
Avant de transmettre des données, l'émetteur et le récepteur doivent se mettre d'accord sur la parité paire ou impaire. Avant d'envoyer chaque paquet de données (chaîne de bits), l'émetteur calcule son bit de parité (0 ou 1) pour s'assurer qu'il correspond à la parité convenue (paire ou impaire). À la réception, le récepteur vérifie la parité des données reçues par rapport à la parité attendue. S'il n'y a pas de correspondance, il y a erreur et les données peuvent être rejetées ou corrigées en demandant une nouvelle transmission.
Le bit de parité n'est utilisé que pour aider à détecter les erreurs, mais il n'a pas la capacité de rectifier les erreurs car il ne peut pas identifier le bit corrompu spécifique. Par conséquent, la seule option pour corriger les erreurs est de rejeter l'ensemble de la chaîne de données et de demander à l'expéditeur de la retransmettre.
Position du bit de parité
Bien qu'il n'y ait pas de règle fixe pour la position du bit de parité, il est généralement ajouté à la fin du message de la chaîne binaire par convention.
Détection des erreurs
Le contrôle de parité au niveau du récepteur permet de repérer les erreurs en comparant la parité du signal reçu à la parité attendue. En cas de non-concordance, le récepteur peut demander une retransmission à l'émetteur.
L'opérateur Modulo permet de déterminer si le nombre de 1 dans une chaîne de données binaires est pair ou impair. Modulo, ou "mod", est une opération mathématique qui permet de trouver le reste lorsqu'un nombre entier est divisé par un autre. L'opération Modulo est représentée par le symbole %.
En utilisant Modulo, nous pouvons déterminer si un nombre est pair s'il peut être divisé par 2 sans laisser de reste. En revanche, si un nombre laisse un reste lorsqu'il est divisé par 2, il est considéré comme impair.
L'exemple de programme C suivant illustre le processus de vérification de la parité à l'aide de modulo :
#includeint main() { unsigned char byte; int num_ones = 0; printf("Enter a byte (in decimal): "); scanf("%hhu", &byte); // Count the number of 1s in the byte for (int i = 0; i < 8; i++) { if ((byte >> i) & 1) { num_ones++; } } // Detect parity with mod 2 and print the parity type. if (num_ones % 2 == 0) { // printf("Even parity\n"); } else { printf("Odd parity\n"); } return 0; }
Le programme commence par lire un octet de l'utilisateur. Il utilise ensuite une boucle pour compter le nombre de bits 1 dans l'octet. Pour ce faire, il décale l'octet vers la droite de chaque position de bit (0 à 7) et vérifie si le bit résultant est 1. Si c'est le cas, le nombre de bits 1 est incrémenté. Enfin, le programme vérifie si le nombre de bits 1 est pair ou impair et imprime le message approprié.
Notez que le programme utilise un char non signé pour stocker l'octet, qui est un entier de 8 bits pouvant contenir des valeurs comprises entre 0 et 255. Le spécificateur de format %hhu est utilisé avec scanf() pour lire une valeur d'octet à partir de l'utilisateur.
Comment ajouter un bit de parité
Examinons un exemple dans lequel nous devons transmettre la chaîne de données 1100101. Tout d'abord, nous comptons le nombre de 1 dans la chaîne de données et déterminons si le nombre est pair ou impair en utilisant l'opérateur mod avec 2 comme diviseur :
(1+1+0+0+1+0+1) mod 2
4 mod 2 = 0
Puisque 4 divisé par 2 n'a pas de reste, le résultat est 0, ce qui indique que nous avons un nombre pair de 1. Si nous avons convenu d'une parité paire, nous ajoutons un "0" comme bit de parité à la fin du message, ce qui donne 11001010, qui peut maintenant être envoyé. En revanche, si nous avons convenu d'une parité impaire, nous inversons le bit de parité et ajoutons un "1" à la place, ce qui donne 11001011 comme message final pouvant être transmis.
Utilisation du bit de parité
- Détection des erreurs: L'une des principales utilisations des bits de parité est la détection des erreurs lors de la transmission des données.
- Stockage en mémoire: Les bits de parité sont également utilisés dans les systèmes de mémoire des ordinateurs pour détecter les erreurs lorsque les données sont stockées dans la mémoire. Lorsque des données sont stockées en mémoire, il existe toujours un risque d'erreurs dues à divers facteurs tels que les interférences électromagnétiques, les défaillances matérielles, etc.
- Systèmes RAID: Le bit de parité est également utilisé dans le système RAID (Redundant Array of Inexpensive Disks). RAID peut également être appelé "Redundant Array of Independent Drives" (matrice redondante de disques indépendants). Les systèmes RAID utilisent plusieurs disques pour stocker les données de manière redondante et se protéger contre les défaillances des disques. Ils utilisent la parité pour la tolérance aux pannes.
En savoir plus : EMI (interférence électromagnétique)
Conclusion
En conclusion, le bit de parité est un mécanisme de détection d'erreurs simple mais efficace qui peut contribuer à garantir la précision du stockage et de la transmission des données. Bien que les bits de parité ne soient pas infaillibles et ne puissent détecter que certaines erreurs, ils restent utiles pour de nombreuses applications dans les communications de données binaires.


